Harmonic oscillator
The local-realistic model of quantum mechanics we are presenting in this blog can adequately describe external force fields. A first example (constant force) has been discussed in the latest post. Among the other possible force fields that particles can experience, a classical textbook example is the Quantum Harmonic Oscillator (QHO), which we shall discuss here.
A QHO is defined by an effective "force" f that varies with the position in the lattice, according to the rule
where Ω is a parameter and x is counted from the center of the force field. The expected position under this force is obtained as
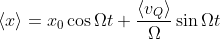
&space;=&space;\frac{1}{2}\frac{d\left&space;\langle&space;v_Q&space;\right&space;\rangle}{d\left&space;\langle&space;x&space;\right&space;\rangle}&space;=&space;\frac{\Omega}{2\left&space;|&space;\sin\Omega&space;t&space;\right&space;|} "\rho(\left \langle x \right \rangle ;t) = \frac{1}{2}\frac{d\left \langle v_Q \right \rangle}{d\left \langle x \right \rangle} = \frac{\Omega}{2\left | \sin\Omega t \right |}")
A QHO is defined by an effective "force" f that varies with the position in the lattice, according to the rule
This result is useful to calculate the probability densities a priori, using the procedure discussed in this post.
We turn now our attention to simulation of a few scenarios, which are discussed in the 2017 ArXiV paper. We use a value Ω = 0.005. In the first scenario, particles of the ensemble are emitted from a single source, so that only the external force is acting (no quantum forces). In this case, the quantum momentum vQ coincides with the source momentum v0, which has a uniform probability distribution. From the rules of compound probability already discussed in an earlier post, we know that it should be
which is a uniform distribution within the range of nodes that are reachable with v0=±1, i.e., the nodes between x0cos(Ωt)+sin(Ωt)/Ω and x0cos(Ωt)-sin(Ωt)/Ω. The numerical simulation using the accelerated code shown here (with the appropriate formulation for the force) confirms this result.
An even more interesting scenario is when the source setting describes a stationary state, which will be described in a future post.
In the second simulation, we prepare a Gaussian wave, that is, a number Ns = 101 of possible sources and a phase momentum vm = 0.1. After Nt = 200 iterations, the "wave" center has moved of a quantity that approximates the theoretical value vmsin(ΩNt)/Ω = 16.8 and the wave as a whole has spread as confirmed by the simulation (the red curve is the theoretical density distribution).
An even more interesting scenario is when the source setting describes a stationary state, which will be described in a future post.
Comments
Post a Comment